CE-marking of collectors
Products
Test Labs
Certification bodies
Scheme Rules
Standards
CE-marking of collectors?
Keymark & OBL/OEM
Misuse of Solar Keymark
Equivalent materials
Solar Keymark Network
Solar Keymark II Project (2006-2007)
Solar Keymark I Project (2000-2003)
Contact
Abbreviations
Miscellaneous
CE-marking related to Pressure Equipment Directive (PED)
As solar collectors are pressurized, the question arises if they are touched by the regulations of the EU pressure equipment directive (PED).According to the rules and guidelines referred below:
- Large collector modules with PS*V BIGGER THAN 50 bar*litres SHALL be CE-marked in relation with the PED
- Normal collector modules with PS*V LOWER THAN 50 bar*litres CAN NOT be CE-marked in relation to the PED
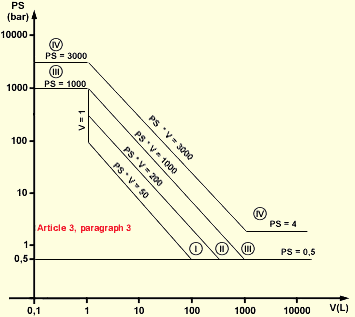
PS: Maximum allowed pressure in bars; V: Volume (fluid content) in litres
It is seen that far most collectors are covered by the Article 3 Paragraph 3, stating: "Such equipment and/or assemblies must not bear the CE marking ...".
However, in some cases CE-marking of solar thermal collectors is obligatory according to the curves above (large collector modules):
- Collector volume in litres multiplied by the max. allowable pressure in bars > 50 litre*bar: Category I - Conformity Assessment Procedures: Module A applies
- Collector volume in litres multiplied by the max. allowable pressure in bars > 200 litre*bar: Category II - Conformity Assessment Procedures: Modules A1, D1, E1 applies
Page updated 24/8 2007.